Chapter 14 Respiration kinetics at the sediment-water interface

Chapter summary:

14.1 The spatial scale of redox sequence in wetlands

In Chapter 8 we presented the theoretical cascade of redox reactions in wetlands. The redox cascade was simplified in a series of well identified spatial zones in which an electron acceptor would be at play. It is the imbalance between the supply and demand of the electron acceptors that defined the zones themselves, and also the direction of concentration gradients and fluxes of electron acceptors and byproducts of respiration (see Figure 8.15). For illustration purposes, the depth and extent of each of the redox layer appeared the same and of several centimeter thick. But is that so, and does it matter?

14.2 Deriving of \(O_2\) microprofile equation in sediment

The hypothesis given is that the volumetric respiration rates are constant, which means that the volumetric respiration rates are of zero order rates with respect to dioxygen in the water column. The dimensions of this rate are \([M.L^{-3}.T^{-1}]\). The instructions given are that the x axis is tilted upward, contrary to what was done in class. The method to derive this equation is to calculate a mass balance for an elementary volume of sediment. Let us take this elementary volume as being a straight parallelepiped of height \(dx\) and of flux surface area \(A\).

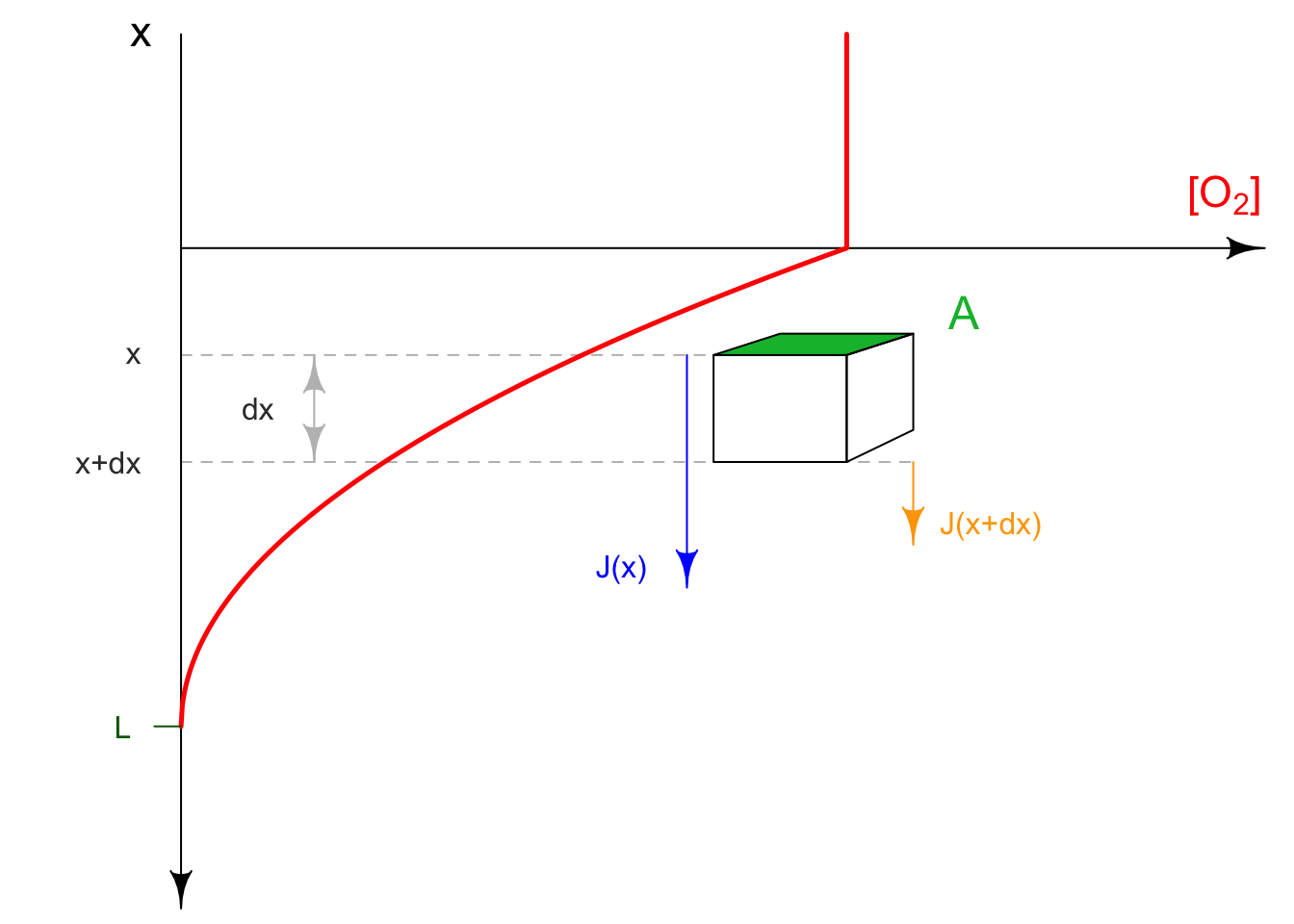
This mass balance can be calculated two different ways. The mass \(\Delta M\) of oxygen removed during \(\Delta t\) is equal to the absolute difference in the downward flux of oxygen \(J(x+dx)\) at \(x+dx\) minus that \(J(x)\) at \(x\). The difference between what was done in class is that both \(J(x+dx)\) and \(J(x)\) are negative this time and the absolute value of \(J(x+dx)\) is greater than that \(J(x)\). So \(\Delta M\), which must be positive, can be calculated as:

\[\begin{equation} \Delta M = \left[ J(x) - J(x+dx) \right].A. \Delta t \end{equation}\]

This is opposite from what was done in class, where the axis was pointing downward.

The mass of oxygen removed \(\Delta M\) can also be calculated from the volumetric removal rate \(R_0\) during \(\Delta t\) such that

\[\begin{equation} \Delta M = R_0 . A . dx . \Delta t \end{equation}\]

Combining these two equations yields

\[\begin{equation} \left[J(x) - J(x+dx)\right].A. \Delta t = R_0 . A . dx . \Delta t \end{equation}\]

Rearranging the equation yields:

\[\begin{equation} \frac{J(x+dx) - J(x)}{dx} = -R_0 \end{equation}\]

Interestingly, this expression is the same one as that seen in class. Taking the limit of this equation when \(dx \to 0\)

\[\begin{equation} \lim_{dx\to 0} \frac{J(x+dx) - J(x)}{dx} = -R_0 \end{equation}\]

yields the derivative of the flux such that

\[\begin{equation} \frac{dJ}{dx} = -R_0 \end{equation}\]

For the expression of the flux down, we use Fick’s law

\[\begin{equation} J(x) = -D\frac{dc}{dx} \end{equation}\]

where \(\frac{dc}{dx}\) is the \(O_2\) concentration (\(c\)) concentration gradient with respect to \(x\), and \(D\) is the diffusivity coefficient. The sign of this equation does not change regardless of the direction of \(x\). Indeed, for a positive \(dx\), the oxygen concentration increases, so \(dc>0\). As a result, \(\frac{dc}{dx}>0\). As result, \(-D\frac{dc}{dx}<0\), i.e., \(J(x)<0\), which is correct using this direction for the axis. The derivative of the flux can thus be written as:

\[\begin{equation} \frac{dJ}{dx} = -D\frac{d^2c}{dx^2} \end{equation}\]

Putting everything back together yields:

\[\begin{equation} \frac{d^2c}{dx^2} = \frac{R_0}{D} \\[7pt] \end{equation}\]

Taking the integral a first time yields:

\[\begin{equation} \int_{}^{} \frac{d^2c}{dx^2} = \frac{dc}{dx} = \frac{R_0}{D}x + a \\[7pt] \end{equation}\]

and finally

\[\begin{equation} c(x) = \frac{R_0}{2D}x^2 + ax +b \\[7pt] \end{equation}\]

where \(a,b,c\) are variables to be determined.

To do so, one looks at the conditions at the boundaries. At \(x=0\), \(c(0) = c_0\), hence \(b = c_0\). At depth \(x = L\) (\(L\) is negative here because the x axis is reversed), both \(c(L) = 0\), and, \(\frac{dc}{dx}(L) = 0\) because the profile is a parabola. One can thus write, using the derivative \(\frac{dc}{dx}(L) = 0\) at the boundary:

\[\begin{equation} 0 = \frac{R_0}{D}L + a \\[7pt] or \\[7pt] a = -\frac{R_0}{D}L \end{equation}\]

Using \(c(L) = 0\) boundary condition:

\[\begin{equation} 0 = \frac{R_0}{2D}L^2 - \frac{R_0}{D}L^2 + c_0 \\[7pt] or \\[7pt] 0 = -\frac{R_0}{2D}L^2 + c_0\\[7pt] and \\[7pt] \frac{R_0}{2D}L^2 = c_0 \end{equation}\]

\[\begin{equation} L^2 = \frac{2c_0D}{R_0}\\[7pt] and \\[7pt] L = -\sqrt{\frac{2c_0D}{R_0}} \end{equation}\]

Because \(L\) is negative. Thus

\[\begin{equation} a = -\frac{R_0}{D} \times -\sqrt{\frac{2c_0D}{R_0}}\\[7pt] a = \sqrt{\frac{2c_0R_0}{D}}\\[7pt] \end{equation}\]

Hence the final equation

\[\begin{equation} \boxed{ c(x) = \frac{R_0}{2D}x^2 +\sqrt{\frac{2c_0R_0}{D}}x +c_0 \\[7pt] } \end{equation}\]

It is possible to verify the answer by replacing \(x\) in the equation derived in class by \(-x\).

14.3 Equation of the downward flux at the sediment-water interface (10 points)

The general expression of the flux down is given by Fick’s law:

\[\begin{equation} J(x) = -D\frac{dc}{dx} \end{equation}\]

From the equation of \(c(x)\), one can calculate the derivative of \(c(x)\)

\[\begin{equation} \frac{dc}{dx} = \frac{R_0}{D}x +\sqrt{\frac{2c_0R_0}{D}} \end{equation}\]

Hence:

\[\begin{equation} J(x) = -R_0x -\sqrt{2c_0R_0D} \end{equation}\]

The downward flux of oxygen at the sediment water interface, which one may call Sediment Oxygen Demand (SOD), corresponds to \(J(x=0)\).

\[\begin{equation} \boxed{ SOD= -\sqrt{2c_0R_0D} } \end{equation}\]

As expected, the flux is negative compared to the direction of the axis. This verification confirms the result obtained.

Figure 14.1: Dioxygen and nitrate concentrations at the sediment water interface in the case of zero order respiration rates in the sediment. The area of the colored rectangles are a graphical representation of the downward fluxes of oxygen and nitrate in the sediment. The value of the nitrate concentration at the interface between the aerobic and denitrification zones has been added, as well as the value of the oxygen (Sediment Oxygen Demand - SOD) and nitrate (JNO3) downward fluxes in the sediment expressed in common reported units. Also available at this link